Algunos apuntes sobre acústica en la música

Distinción entre sonidos simples y complejos

Los sonidos simples, también llamados puros, son aquellos que tienen una única frecuencia, como por ejemplo un diapasón. Cuando damos un golpe a un diapasón, se producirán 440 vibraciones por segundo (de ahí procede el término "afinación a 4.40"). Estas 440 vibraciones por segundo darán como resultado la nota la. El concepto de vibración por segundo aparece por vez primera en el siglo XVI con la revolución científica y con personalidades como Galileo o Deckart. Por lo general, los sonidos puros no son agradables al oído (como el pitido de aviso de cierre de puertas de un metro, por ejemplo, que también sería un sonido simple); tampoco es fácil detectar el foco de origen de los sonidos puros (si en una habitación se emitiera un sonido puro y tuviéramos los ojos cerrados no sabríamos desde dónde se está emitiendo).

Los sonidos complejos son el resultado de la suma de varios sonidos puros.

En acústica nombramos cada una de las octavas con un subíndice numérico, de tal modo que consideramos el do central del piano como el do4 y según subimos en la escalas subimos en número (do5, do6...) y según bajamos en la escala bajamos también el subíndice (do3, do2...)

Con el cuadro de la serie de armónicos delante, podemos expresar cualquier intervalo con una proporción (y esto entronca directamente con las teorías pitagóricas). De tal modo que, por ejemplo, una octava se expresa con la proporción 2:1, una quinta (do y sol) con la proporción 3:2 y una tercera mayor (do y mi) con la proporción 5:4. Esto se visualiza y comprende mejor si pensamos en una cuerda tensada. Si percutimos esa cuerda sonará una determinada nota, si dividimos esa cuerda por la mitad y la percutimos, sonará la octava de esa nota; si la dividimos en 3 partes, con dos de sus tercios obtendremos un quinta justa. Algunos armónicos están en negro, más adelante veremos por qué.

Podemos comprobar el funcionamiento de los armónicos sentándonos delante de un piano acústico. Si tocamos el do2 del piano, automáticamente oiremos un quinta justa, sin necesidad de tocarla. Para los duros de oído, podemos mantener presionada la tecla del sol3, sin llegar a producir sonido, tan solo para levantar el macillo. Después tocaremos de nuevo el do2. La vibración del sonido del do2 excitará la cuerda del sol3.

A partir de la tabla de serie de armónicos, podemos plantear una serie de problemas y deducir qué notas darán determinadas longitudes de cuerda de un violín o determinadas longitudes del tubo de un instrumento de viento. Veamos un par de problemas y sus soluciones:

¿Cómo calcular una nota a través de la longitud de una cuerda?
Es sencillo, sólo tenemos que tener en mente las proporciones de la serie de armónicos. Imaginemos una cuerda de 12 cm que al frotarla nos da un la bemol, ¿cuánto nos dará una cuerda que mida 60 cm? Establecemos la relación entre ambas cuerdas: 60/12 = 5/1. La proporción es de 5/1, si vamos a la tabla de la serie de armónicos y vemos cuál es esa proporción, veremos que es la de una tercera mayor descendente a la doble octava inferior. Por tanto, la nota que obtendremos al frotar una cuerda de 60 cm es un fa dos octavas grave del la bemol.

Pongamos otro ejemplo, si ese mismo trozo de cuerda de 12 cm me da un la bemol, ¿cuánto me darán 20 cm.? Hacemos el mismo proceso, averiguamos su proporción: 20/12 = 5/3. Si vamos a la tabla de armónicos, veremos que la proporción 5/3 es la de una sexta mayor descendente. Por lo que nuestra cuerda de 20 cm nos dará un do bemol.

Si tenemos un tubo cerrado que mide 60 cm que nos da un do, ¿qué nota dará ese mismo tubo si mide 10 cm? El procedimiento es muy similar a las cuerdas del violín. Tenemos que fijarnos en la proporción. La proporción es de 10/60, que simplificándolo, se queda en 1/6. Es decir, con ese mismo tubo midiendo 10 cm, la nota que obtendríamos sería la del sexto armónico, que si vamos a la tabla veremos que es la quinta dos octavas aguda. Por lo tanto, la nota que obtendríamos sería la nota sol, que es la quinta de la nota sol que nos da el tubo con 60 cm.

Ahora un poco más simple: ¿qué nota dará un tubo de 60 cm? Tendríamos que calcular la frecuencia, que es igual a la velocidad de propagación del sonido (343) dividida por la longitud de onda. La longitud de onda la calculamos multiplicando 60x0'02= 1'2

F=343/1'2= 285

Vamos a ponerlo ahora más difícil. ¿Qué nota da un tubo cerrado de 50 cm en el tercer modo de vibración? Cuando hablamos de un tubo cerrado, nos referimos a que sólo da los armónicos pares y cuando hablamos del tercer modo de vibración, estamos hablando del quinto armónico. Podemos calcularlo de la siguiente manera:

Dado que la frecuencia es igual a la velocidad de propagación del sonido dividida por la longitud de la onda, averiguamos la frecuencia de la nota de la fundamental. Sabemos que la velocidad de propagación es de 343 y que la longitud de la onda es 0'5 m (los 50 cm) x 4=2

F=343/2=171 hercios

Esta sería la frecuencia de la fundamental. Para saber ante que nota nos encontramos, podemos multiplicar por dos esta frecuencia (multiplicar por dos la frecuencia sólo implica cambiarla a una octava más grave). Multiplicamos por dos sólo para acercarla a un frecuencia que conocemos, el la central del piano, que son 440 hercios. 171x2=342... esta frecuencia se aproximaría más o menos a un fa. Dado que el quinto armónico es la tercera mayor, podemos atrevernos a decir que la nota que da un tubo cerrado de 50 cm en el tercer modo de vibración es un la "más o menos".

Temperamento igual

El temperamento igual fue el sistema de afinación que se impone a mediados del siglo XVIII dado que la serie de armónicos natural deja de ser viable. La música anterior a esta época no utiliza el temperamento igual. Este sistema se basa en la división de la octava en doce partes proporcionalmente iguales basadas en el semitono y de aquí se deduce esta fórmula: 

2^1/12 =¹²√2

No obstante, entre notas de diferente nombre hay un semitono más grande que entre notas con mismo nombre. Es decir, la distancia entre la y sol# es más grande que entre sol# y sol natural. Incluso el propio Mozart decía que no todos los semitonos eran iguales.

El temperamento igual obligó a disminuir el intervalo de quinta justa para que las terceras no sonaran desafinadas. Esto significa que una quinta pitagórica no es igual a una quinta en el sistema de temperamento igual. ¿Cómo lo podemos comprobar? Haciendo el cálculo en ambos sistemas.

En el temperamento igual
Teniendo en cuenta que el semitono es ¹²√2, multiplicaremos por 7, puesto que ese es el número de semitonos que hay en una quinta justa. Partiendo del La4, vamos a calcular los hercios de su quinta justa (el Mi5), y para ello simplemente multiplicaremos 440 x (¹²√2)^x7


El resultado es 659'255 hercios.


En el sistema de afinación justa
Veamos qué sucede ahora en el sistema de afinación justa. El cálculo es más sencillo que en el temperamento igual, solo hay que multiplicar 440 por la proporción del intervalo de quinta de la serie de armónicos, que en el caso de la quinta justa es 3:2 (o 6:8 o 12:8).

440 x 6/4=660 hercios.

Como podemos observar, hay una pequeña diferencia entre ambos sistemas de afinación (de 0.745 hercios). Diferencia tal vez imperceptible para el oído humano, pero que se queda en evidencia cuando se hace el cálculo matemático.

En el siglo XIX se inventó un sistema logarítmico: el cent, que equivale a una centésima de semitono ⁽¹²√2) 

Por lo tanto, en el temperamento igual:

- Una segunda mayor serán 200 cents
- Una tercera menor serán 300 cents
- Una tercera mayor serán 400 cents
- Una cuarta justa serán 500 cents
- Una quinta justa serán 700 cents
- Una séptima menor serán 1000 cents

Para calcularlo en el sistema natural, utilizaremos la siguiente fórmula:

c= log (m/n) / log 2 x 1200

Donde el logaritmo de m/n es la razón de un intervalo en la serie de armónicos. Calculemos entonces cuántos cents tiene una tercera mayor ( 5:4) en el sistema temperado:

c= log (5/4) / log 2 x 1200 = 386.3

Si comparamos ambos resultados (400 cents y 386.3 cents), observamos que hay una notable diferencia entre el sistema de afinación justa y el temperamento igual, siendo la terceras mayores más altas en la afinación justa.

Calculemos ahora la quinta justa por el mismo procedimiento:

c=log (3/2) / log 2 x 1200 = 702

Es decir, la quinta justa tiene 2 cents más en el sistema natural que en el sistema de temperamento igual. Esto quiere decir que las quintas natural son más grandes que las quintas del sistema temperado. No obstante, también es cierto que el oído humano no percibe grandes diferencias a menos de 5 cents.

Ahora vamos a retroceder un poco en nuestros apuntes. Si recordáis la serie de armónicos arriba expuesta, veréis que hay dos notas en negro: la séptima menor (sib) y fa #. Vamos a calcular en ambos sistemas, cuantos cents tiene ese sib:

En el temperamento ajustado: como la séptima menor contiene un total de 10 semitonos, su total de cents es 1000 (100 x 10 = 1000)

En el temperamento igual: c= log (7/4) / log 2 x 1200 = 968 cents

De nuevo nos encontramos con un desfase. Si con las terceras mayores ya era notorio, aquí se hace más que evidente, puesto que es un desfase de 32 cents. ¿Qué implica esto en la realidad? Que un sib dado por un piano sonaría notoramiente más alto que un sib tocado por un instrumento como la flauta, y por consiguiente, este sib nos sonaría desafinado, pese a que es el sib natural.

Veamos ahora qué sucede con el 11º armónico y por qué aparece el # entre paréntesis. Para ello vamos a calcular cuántos cents tiene fa# y cuántos fa natural.

Fa# tiene 600 cents (puesto que hay 6 semitonos desde do hasta fa#)
Fa natural tiene 500 cents(puesto que hay 5 semitonos desde do hasta fa natural)

Ahora calculemos el número de cents en el temperamento igual:

c= log (11/8) / log 2 x 1200 = 551 cents

En el sistema de temperamento igual el 11 armónico se encuentra a mitad de camino entre el fa natural y el fa#.

Arriba hemos dicho que un tono del piano tiene 200 cents, pero ¿cuántos cents es en el sistema natural? Hagamos el cálculo tomando como referencia la relación de tono entre el 9º y 8º armónico (entre las notas re y do).

c= log (9/8) / log 2 x 1200 = 203,9 cents

De nuevo, el tono en el sistema natural es más grande que en el sistema temperado. No obstante, hagamos ahora el cálculo teniendo en cuenta la razón de los armónicos 10º y 9º ( entre mi y re):

c= log (10/9) / log 2 x 1200 = 182,4 cents

Esto entroncaría con el espectralismo.

Stockhausen utiliza en una de sus obras este intervalo: ²⁵√5; es decir, divide el intervalo que hay desde el do2 y el mi4 en 25 partes. ¿Cómo sabemos que es este intervalo? Es sencillo, la raíz cuadrada de 5 se refiere al 5º armónico (o sea, mi). Si hacemos al cálculo, descubriremos que la unidad de temperamento del sistema de Stockhausen es más grande que en el sistema temperado (es decir, que el semitono).

c= log (²⁵√5)/ log 2 x 1200 = 111,45 cents

La tensión de una cuerda está relacionada con la altura de la nota, cuanto mayor sea la tensión, mayor será la altura de la nota y viceversa. Si multiplicamos la tensión por dos, la altura sube √2; si la multiplicamos por 25, subirá √25. Si multiplicamos por 4 la tensión, obtendremos la octava. El tamaño de la cuerda también influye en la frecuencia y por tanto en la nota. Pensemos en las cuerdas del piano, por ejemplo, las notas más agudas se corresponden con las cuerdas más finas, mientras que las notas más graves se corresponden con las cuerdas más gordas. Si una cuerda es dos veces más gorda, será √2 más grave.

A partir de lo que hemos visto, si nos aprendemos de memoria estos tres datos que a continuación pongo, podremos calcular rápidamente cuántos cents tiene en la afinación justa el resto de intervalos:

La octava=1200 cents
La quinta= 702 cents
La tercera mayor= 386

De tal forma que para calcular una cuarta, solo tendremos que restar una quinta a la octava: 1200-702=498 cents

Fenómenos ondulatorios

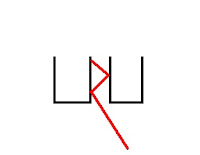
1. Reflexión: el dibujo es un poco rústico, pero expresa de forma esquemática el fenómeno de la reflexión, en el que el ángulo de entrada es igual al ángulo de salida.

En las superficies curvas, todos los rayos tienden a concentrarse en un punto focal.

Las superficies convexas son las mejores para el aspecto sonoro. Este fenómeno lo tienen los teatros italianos de ópera, ya que los palcos son excelentes difractores del sonido.

En las iglesias elípticas ocurre esto:

La reflexión en una cámara anecoica, no existe, dado que las condiciones que en ella se dan no permiten la reflexión en las paredes. Una onda se refleja si es igual o más pequeña que su superficie. En una cámara anecoica, los rayos se escapan por ranuras y se convierten en calor.

John Cage ideó su obra 4'33'' en una cámara anecoica.

El fenómeno de la reflexión también está muy ligado con el término impedancia, que es el impedimento que ofrece un objeto a la propagación de las ondas. Su símbolo es Z y es dependiente de la frecuencia. Se expresa así:

Z (f)=Fuerza/ velocidad

Si la misma fuerza necesita la misma velocidad, tiene menos impedancia. Supongamos una cuerda a la que se le suma una cuerda mas grande

Si a esa cuerda le damos un pulso, parte de la energía se transmitiría a la cuerda grande y otra parte iría en dirección contraria.

Cuanto mayor sea la impedancia, mayor energía vuelve hacia atrás. Esto es un concepto que entronca con el momentum. De aquí deducimos la siguiente fórmula:

R (cantidad de reflexión)= (Z1-Z2)²/ (Z1+Z2)²

En la que Z1 es la impedancia del objeto 1 y Z2 es la impedancia del objeto 2. Esto tiene que ver mucho con los instrumentos musicales; cada instrumento musical tiene un nivel de impedancia, dado que es necesario que haya una reflexión del sonido. Si pasara toda la energía, no se podría mantener una nota concreta. Por ello, el puente de un violín o la campana de una trompeta, transmiten la mayor parte del sonido y reflejan una pequeña parte de éste.

El concepto de impedancia podemos encontrarlo incluso en el cuerpo humano. Una de las funciones del oído medio es el de compensar las impedancias, dado que la impedancia del aire es superior a la impedancia del líquido que hay en el oído interno, la perilinfa. El oído medio hace de amplificador aumentando la vibración.

2. Refracción: es el cambio de dirección de un rayo cuando cambia de un medio a otro de diferente densidad. Con el fenómeno de la refracción tenemos dos casos: el primero de ellos es el cambio de la frecuencia de un sonido en función de la temperatura. Sabemos que la velocidad del sonido en el aire, a una temperatura de 0 grados Celsius, es de 331'570 metros por segundo y esta aumenta 0'6 m/s por cada grado más de temperatura. Parejamente, disminuye 0'6 m/s por cada grado menos de temperatura. Partiendo de esta base, imaginemos el siguiente problema: tenemos una flauta de 60 cm. que da un la de 440 Hz, ¿qué nota daría esta misma flauta en el Polo Norte, a -10 grados centígrados? En otras palabras, ¿cuál sería su frecuencia?

Para calcular la frecuencia de la nota la en el Polo Norte, a -10 grados, lo primero que tenemos que calcular es la longitud de onda (λ) en condiciones normales (es decir, a 20 grados). A 20 grados, la velocidad de propagación del sonido es de 443 metros por segundo (0'6x20=12; 12 + 431=443). A esto le dividimos la frecuencia de la nota la (440 Hz): 443/440, dado que la longitud de la onda:

λ= velocidad/frecuencia

El resultado es 0'78.

Una vez calculada la longitud de onda, tenemos que calcular la velocidad de propagación del sonido en el Polo Norte. El procedimiento es el mismo. Si la velocidad aumenta 0'6 m/s por cada grado, la vel. de propagación del sonido en el Polo Norte a -10 grados será de 325 (0'6x10=6; 431-6=325).

Ahora, para calcular la frecuencia, utilizaremos la fórmula arriba expuesta:

Frecuencia= velocidad/ longitud de onda (λ)

Conocemos la velocidad de propagación en el Polo Norte(445 m/s) y conocemos la longitud de onda (0'78). Por tanto:

Frecuencia= 325/0`78; Frecuencia=416'7

Para saber cuánto es esto en cents, tendremos que usar la fórmula vista al principio de la entrada y que recordamos aquí: c= log (m/n) / log 2 x 1200

De tal forma que: log (440/417)/ log 2 x 1200= 92 cents, 

Por lo tanto, en el Polo Norte, la misma flauta daría un la 92 cents más bajo, (que es casi medio tono), que en condiciones naturales,.

El segundo de los casos es la refracción atmosférica: cuanto mayor es la temperatura, a mayor velocidad se propagan las ondas del sonido y viceversa.

3.Difracción: es la capacidad que tienen las ondas de atravesar los obstáculos. Si la longitud de onda es menor que el objeto, se da la reflexión; si es mayor, la onda continua y lo atraviesa. El fenómeno de la difracción es importante para entender la propagación de los sonidos graves y agudos. Pongamos el ejemplo del coche que pasa con la música a toda caña; en este caso, sólo escucharemos las frecuencias más graves, que son las que tienen una longitud de onda más grande y por tanto pueden atravesar las paredes del coche, mientras que las frecuencias agudas, de longitud más pequeña, no logran atravesar la pared del coche y sólo las escucharemos si alguien baja la ventanilla.

4. Interferencia de las onda. Existen dos tipos: la interferencia constructiva y la interferencia destructiva. Ambos fenómenos se pueden visualizar en este vídeo de Youtube.

Fenómeno de los batimientos
Los batimientos, usados por los afinadores, surgen cuando tenemos dos frecuencias muy cercanas entre sí (como por ejemplo una frecuencia de 400 Hz y otra de 388Hz). No obstante, cuando estemos afinando un piano también puede haber batimientos entre dos notas muy separadas entre sí, como do y sol, distancia de quinta. ¿Por qué se producen estos batimientos? Por sus armónicos:


En una cuarta son más difíciles de escuchar porque están más lejos de la fundamental:

Efecto Doppler
El efecto Doppler se explica muy bien con el ejemplo de la sirena de una ambulancia. A todos nos ha ocurrido alguna vez que, paseando por la calle, ha pasado un ambulancia a toda velocidad con la sirena encendida y según se acercaba a nosotros el sonido se escuchaba muy agudo y según se alejaba lo oíamos más grave. Esto ocurre así porque las longitudes de onda más cortas se acumulan delante de la ambulancia, mientras que las longitudes de onda más largas se quedan por detrás.

¿Qué nota dará un tubo con una longitud de 20 cm en el segundo modo de vibración? (no sé si esto está bien) Podemos realizar el cálculo teniendo en cuenta los siguientes datos:

Para saber qué nota da el tubo, tenemos que conocer la frecuencia. Teniendo en cuenta la siguiente fórmula:

Frecuencia=velocidad/ longitud de onda

y teniendo en cuenta que la longitud de la onda en el 2º modo de vibración es 3/4 de lambda, tenemos ya los suficientes datos como para poder hallarlo.

L=3/4 de lambda; 0,2 m=3/4 de lambda; lambda=0.26

Sabiendo que la velocidad de sonido en el aire es de 340 m/s:

340=0.26 x frecuencia; frecuencia=1275Hz

Problemas para resolver
A continuación, se presentan una serie de problemas para resolver atendiendo a lo expuesto a lo largo de la entrada:

- Si nuestra fundamental es lab, ¿qué armónicos estarían desafinados? Para saber esto, tenemos que tener en cuenta el recuadro de la serie de armónicos del principio de la entrada. Las notas pintadas en negro son los armónicos que sonarán desafinados. Estas notas son la séptima y la oncena, por lo que en lab, las notas que estarán desafinadas serán el solb (la séptima) y el reb (la oncena).

- Si reb es el quinto armónico, ¿cuál será su fundamental? De nuevo tenemos que tener en cuenta la tabla del principio de la serie de armónicos. El quinto armónico coincide con la tercera mayor con respecto a la fundamental, por lo tanto, sólo tenemos que "calcular" una tercera mayor descendente desde reb, que es sib.

- Si una cuerda de 60 cm da la nota lab, ¿qué nota dará 12 cm de esa misma cuerda? Dado que 12 cm, es 1/5 de la cuerda (12/60), y 1/5 se corresponde con el quinto armónico, sólo tendremos que averiguar cuál es el quinto armónico de lab mirando la tabla de la serie de armónicos. De nuevo tenemos que tener en mente la tabla de la serie de quintas. El quinto armónico de lab, que coincide con una tercera mayor, por lo tanto, será do.

- Pon tres maneras de escribir matemáticamente la tercera menor.
440x(¹²√2)<sup>3

3</sup>√2

√2:³√2

- ¿Qué nota dará un tubo de 60 cm?

- ¿Qué nota da una cuerda de 60 cm en su segundo modo de vibración a una velocidad de propagación de 500m/s? Tenemos que tener en cuenta que el segundo modo de vibración, en un tubo abierto, son los armónicos pares; en un tubo cerrado, son los impares. El tercer modo de vibración, en un tubo cerrado, es el quinto armónico.

- ¿Cuánto debe medir un tubo cerrado para que en su segundo modo de vibración dé la nota la5?

- Exprese en cents y matemáticamente en la afinación justa y pitagórica y en el temperamento igual los intervalos de tercera menor, cuarta y semitono diatónico?

La resonancia

Si un objeto vibra es por dos razones: elasticidad y materialidad. A la rigidez le atribuiremos la letra K y a la masa la designaremos con la letra m. La frecuencia a la que vibra una masa se puede calcular mediante esta fórmula:

f=1/2π x √k/m

Un cuerpo capaz de vibrar es sometido a una fuerza periódica, cuyo período de vibración coincide con el periodo de vibración característico de dicho cuerpo. Una fuerza relativamente pequeña aplicada de forma repetida hace que la amplitud del sistema oscilante se haga más grande.

Cuando un objeto vibra, lo hace por una frecuencia concreta: es lo que sucede cuando un cantante rompe una copa de cristal al emitir determinada nota. Para saber en qué frecuencia vibra la copa, haremos un glissando y en determinada frecuencia vibrará. Por ejemplo, el puente de Takoma se rompió porque la vibración del viento coincidió con la vibración del puente. En la resonancia, el cuerpo absorbe energía cuando hay una coincidencia propia del objeto y la frecuencia que le llega desde fuera. 

La rigidez se puede calcular mediante la siguiente fórmula:

k= f/m

Fuerza=-k x m

Pensemos en un muelle que emite la nota do4. ¿Qué nota darían dos muelles de las mismas características que este anterior? Un fa#. Para que nos diera un do3 –una octava aguda con respecto al primero–, tendríamos que poner cuatro muelles del mismo tipo. ¿Cómo podríamos desafinar dos diapasones iguales? Poniéndole a uno de ellos más masa.

El resonador de Helmholtz es un tipo de absorbente acústico creado artificialmente para destruir o absorber un determinado margen de frecuencias. Consiste en una cavidad con un orificio en el extremo de un cuello en cuyo interior el aire se comporta como una masa resonante. Son oquedades que absorben la energía: una ocarina, un tubo de escape de un coche o el silenciador de una pistola... Los resonadores de Helmholtz cuentan con dos cavidades: una para el oído y otra para la fuente. Si la composición del sonido contiene una frecuencia igual o similar a la frecuencia resonante de la cavidad del resonador, ésta se amplificará.

Ondas estacionarias

Una onda es una perturbación que va de un sitio a otro. Cuando no puede seguir, invierte la fase y vuelve hacia atrás. Aparece entonces una interferencia y es lo que hace surgir un patrón de ondas estacionarias. Son un tipo de ondas en las que determinados puntos, denominados nodos, permanecen inmóviles. Resultan de la interferencia de dos ondas de la misma naturaleza, amplitud, longitud de onda (o frecuencia) que avanzan en direcciones opuestas. Las ondas que se encuentran tienen que tener la misma amplitud. Así funcionan los armónicos de un violín. Las ondas estacionarias permanecen confinadas a un espacio. No se puede considerar a las ondas estacionarias como ondas de prolongación, sino como modos de vibración de una cuerda, membrana o tubo de aire. En las cuerdas, por ejemplo, existen determinadas frecuencias en las que se producen ondas estacionarias llamadas frecuencias de resonancia.

Tenemos una cuerda que se mueve a 100 Hz, si aplicamos 50 Hz, la cuerda apenas vibra, según nos acercamos a los 100 Hz, la cuerda vibra de forma más regular. Si nos alejamos de 100 vuelve a vibrar irregularmente hasta los 200 Hz, ya que aquí la cuerda vibraría el doble.

Los nodos son los puntos de máxima presión. Pensemos en un muelle al que tiramos de los lados. Habrá más presión en los extremos que en el centro. Si presionamos en el centro, la presión es mayor en el centro. ¿Por qué un guitarrista no pulsa en la mitad de la cuerda? Porque es el punto del antinodo: es ahí donde se produce el movimiento y el sonido. También influye el hecho de tocar con el pulgar o con una púa. La superficie es mayor con el pulgar y esto restará armónicos y el sonido saldrá más cálido. Con la púa, al estar focalizado en un punto, tendrá más armónicos. Cada armónico es una vibración distinta de cada cuerda.

En el caso del piano, el macillo, cuando golpea la cuerda, se comprime y después se descomprime. Esa descomposición no es lineal. Cuanto más fuerte golpees el macillo, más duro estará y más armónicos superiores sonarán.

Psicoacústica

Es una disciplina que estudia la manera en la que percibimos como raza el fenómeno de las ondas. Hay una serie de reglas que intentan explicar la relación entre el mundo interior y exterior. ¿Cómo funciona el oído humano? El ser humano dispone de dos oídos para saber la procedencia del sonido. Cuando la fuente emite longitudes de onda cortas (sonidos agudos), al ser más pequeñas que la cabeza, estas rebotan y no llegan al otro lado produciéndose una sombra acústica llamada diferencia interaural. Como sabemos, el oído humano se divide en tres partes: el oído externo, el oído medio y el oído interno. El pabellón, situado en el oído externo, tiene una serie de canales y cada uno filtra las ondas. 

Nuestro sistema auditivo está adaptado para escuchar consonantes. Muchas consonantes son determinantes para el habla. El oído está mejor preparado para el lenguaje que para la música.

El oído medio funciona como una conexión entre el oído externo y el interno. Si no hubiese oído interno, la diferencia de impedancias entre el aire y la perilinfa (el líquido del caracol) no permitirían escuchar nada.

Tensor del tímpano: músculo que tensa el tímpano cuando se mueve demasiado.

El reflejo del estribo: si el movimiento del estribo es demasiado rápido, desplaza el estribo fuera de su lugar habitual.

Trompa de Eustaquia: conectada a la garganta.

El órgano Corti es el órgano sensitivo del oído y puede considerarse como el micrófono del cuerpo.

La percepción de la intensidad sonora

Utilizamos los decibelios como medida. Hay dos psicólogos, Weber y Fechner, a los que se les debe la ley Weber-Fechner: mientras el estímulo aumenta geométricamente, la sensación aumenta aritméticamente.

Los decibelios=10 x log (I/I0)

Los decibelios comparan dos cantidades, establecen una relación entre dos cantidades. I0 es la intensidad de referencia. No podemos confundir la intensidad con la sonoridad: en el primer caso, hablamos del medio físico; en el segundo, hablamos de la percepción. La intensidad se mide en vatios por metro cuadrado y el nivel de intensidad se mide en decibelios. La sonoridad se mide en sonios. Aproximadamente 10 dB equivalen al doble de sonoridad.

20 dB=una hoja meciéndose en el prado

40 dB=lo máximo permisible para dormir tranquilamente

60 dB=una conversación normal

80 dB=el tráfico en la Gran Vía de Madrid

90 dB=el tráfico en una autopista

100 dB=una discoteca

120 dB=umbral del dolor

130 dB=avión al despegar

Los decibelios disminuyen con la distancia, 10 dB no se perciben igual a cuatro que a ocho metros.

Curvas de Fletcher y Munson

Las curvas isofónicas son aquellas que tiene la misma sonoridad. Todo lo que está en la línea de abajo se escucha al mismo volumen, aunque los decibelios sean distintos.

Enmascaramiento del sonido

Hablamos de enmascaramiento del sonido cuando un sonido elimina a otro: cuando pasa un avión y tapa la voz de alguien hablando. Distinguimos el preenmascaramiento, el enmascaramiento simultáneo y el postenmascaramiento. El preenmascaramiento se da en situaciones en las que determinado ruido tiene un ancho de banda y provoca la modificación de la línea. Los sonidos con menor intensidad no se oirán. En el enmascaramiento simultáneo, los tonos muy cercanos en frecuencia se enmascaran más fácilmente que tonos puros más alejados. Los sonidos graves enmascarán a los sonidos agudos con más facilidad.

Percepción de la altura y el timbre

No es lo mismo la frecuencia que la altura, aunque están relacionadas: cuanto mayor sea la frecuencia, mayor es la altura del sonido. Las personas que son incapaces de distinguir una altura de otra padecen de amusia. El intervalo de octava es privilegiado. Se debe a fundamentos psicológicos. Hay unas escalas que son puramente psicológicas, como la escala melódica, ya que se trata de una escala subjetiva que no se corresponde con las frecuencias. 

Bibliografía

ROSSING, Thomas: The science of sounds, Handcover, 2001

ROEDERER, Juan: Acústica y psicoacústica de la música, Ariel, 2020

GIORDANO, Nicolas: Physics of the piano, Oxford UP, Oxford, 2010

BURRED, Juan José: La acústica del piano

Askenfell, Five piano lessons

Enlaces de interés
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html